Tongpeng Guan

Tongpeng Guan

Stay Curious!

ICU Serum Sodium Prediction

Background：Dysnatremia is a central electrolyte disorder in the intensive care unit (ICU) that results in poor prognosis and increases in-hospital mortality risk. The existing clinical method for estimating serum sodium level is based on the experience of doctors, which is subjective and difficult to predict the patient’s subsequent status. To simplify this difficulty, we aimed to develop an assistance system for doctors to predict short-term serum sodium changes.

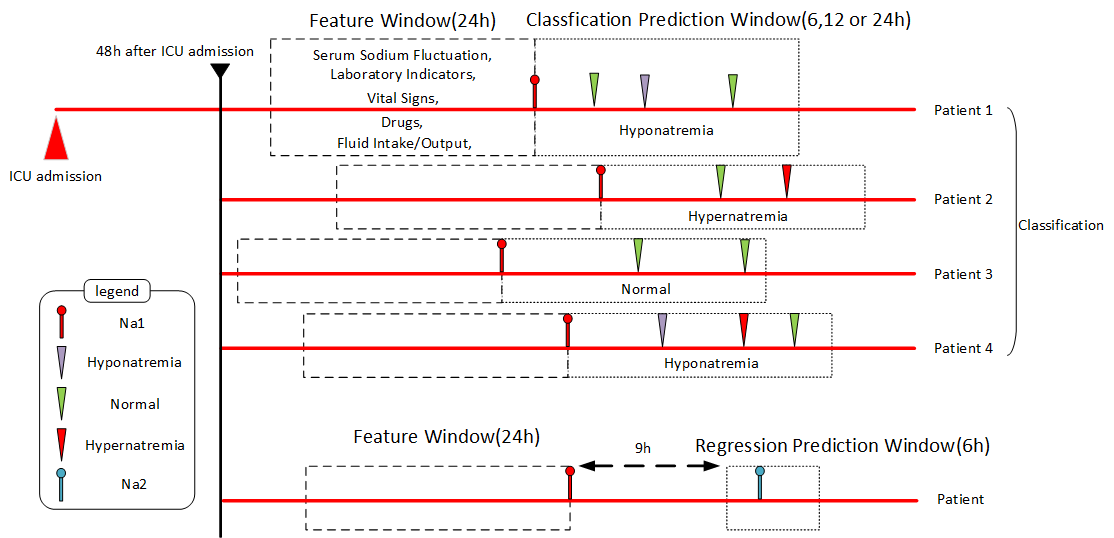
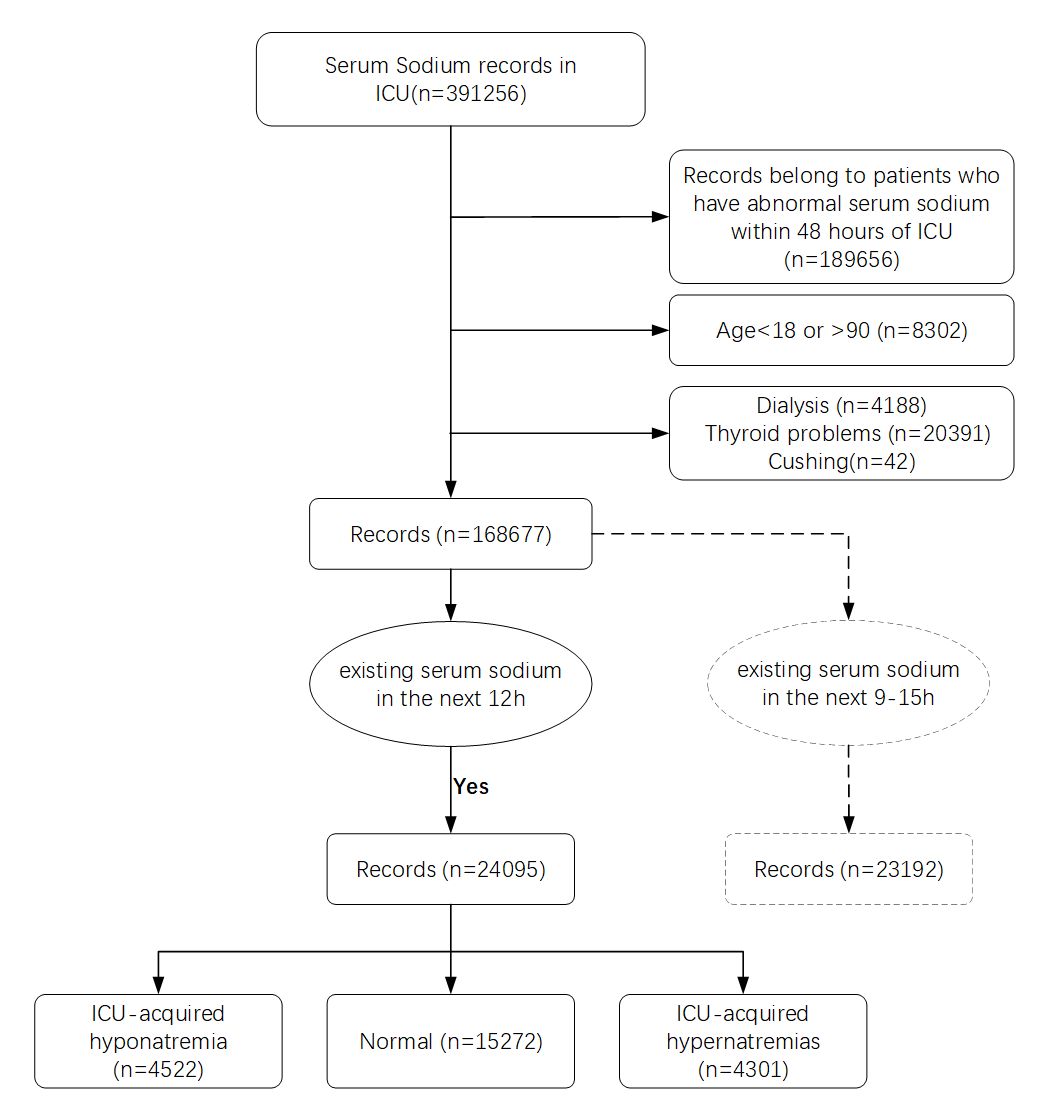
Methods：Patient samples with abundant feature variables were extracted from electronic health records (EHR) using a dynamic sliding window method. The end point of the feature window was the patient’s initial serum sodium record 72 hours after admission, with the starting point set at 24 hours before the end point. Five machine learning classification models were developed based on the patient clinical indicators extracted from the feature window, which were used to predict the subsequent serum sodium status in the prediction window for time intervals of 6, 12, and 24 hours. A regression analysis was performed on the patients’ serum sodium values. The least absolute shrinkage and selection operator regression model was applied for feature selection, and four machine learning models were trained to predict serum sodium values. The prediction results of all models were evaluated and compared, and SHapley Additive exPlanations (SHAP) was utilized to assess the interpretability of the best performing classification and regression model.

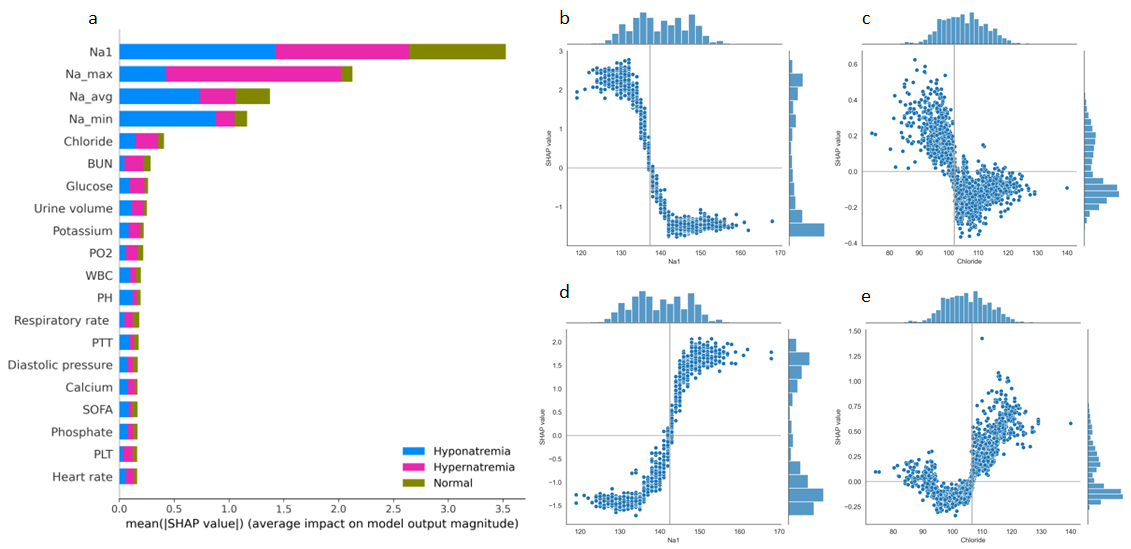
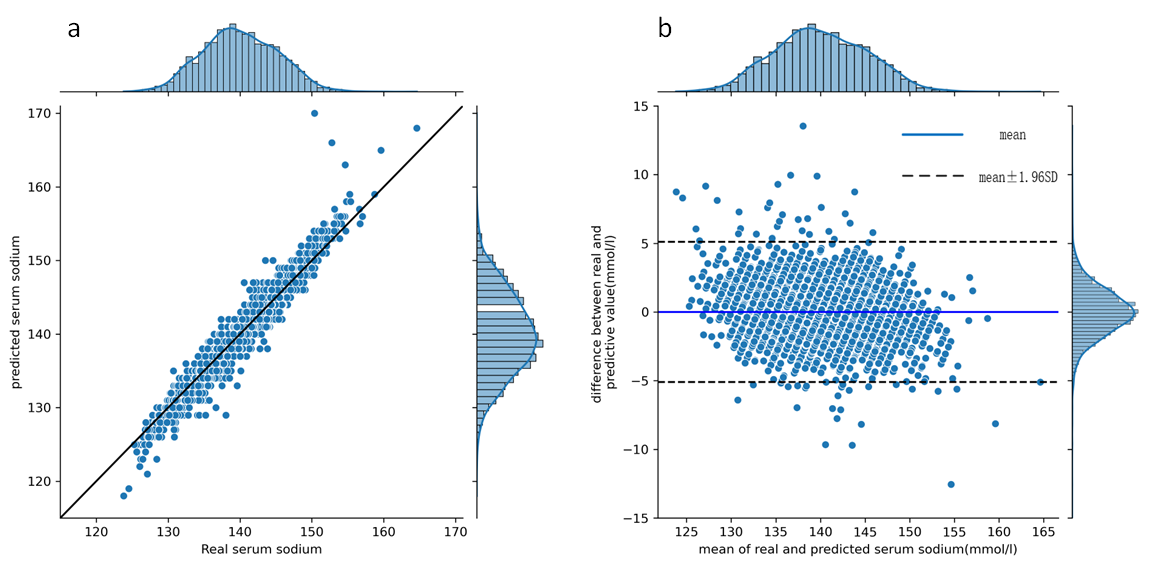
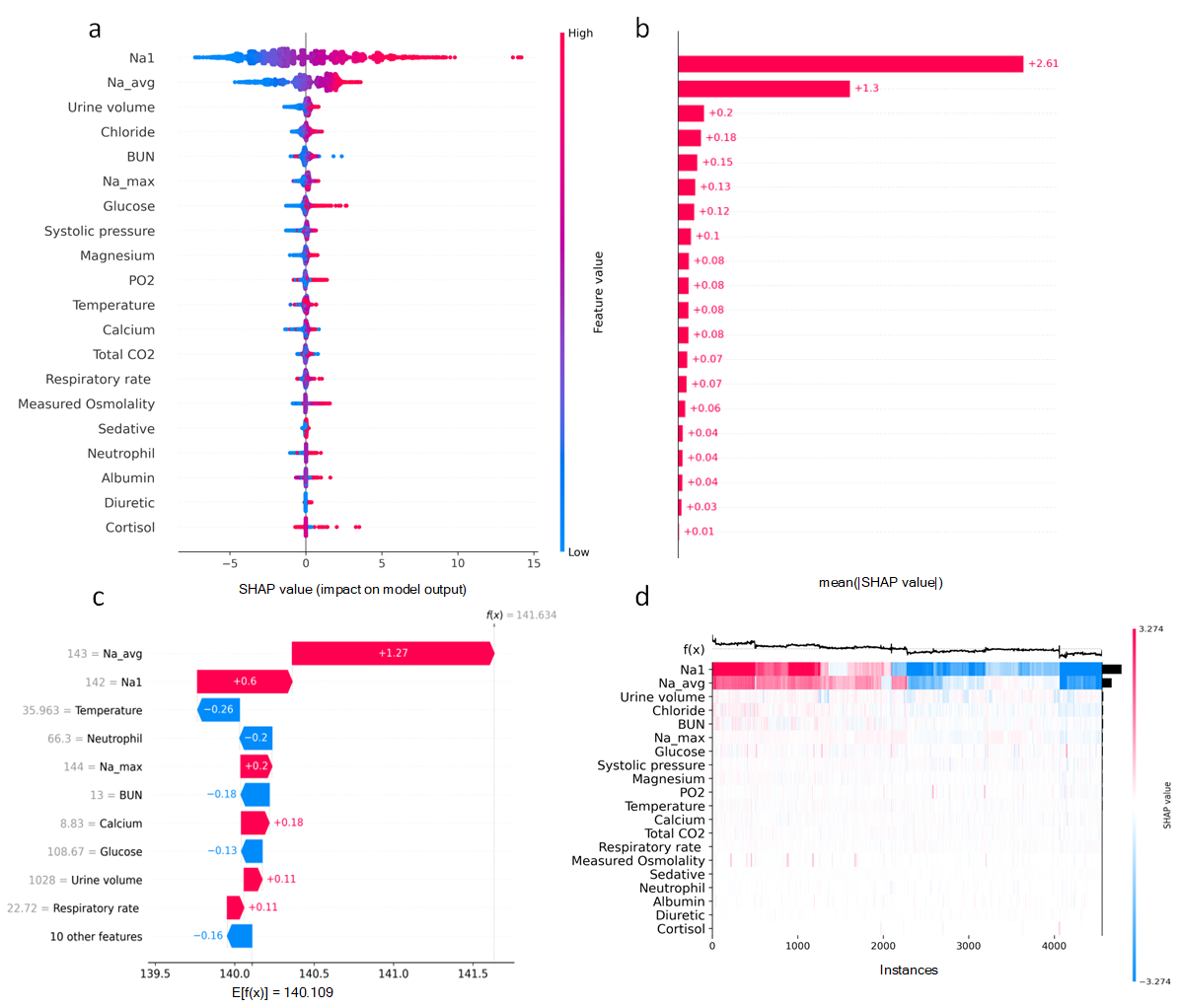
Results：In the 12-hour classification prediction window, there were 4522 hyponatremia samples, 15272 normal serum sodium samples and 4301 hypernatremia samples. Among the classification models, the best model was LightGBM with accuracy, sensitivity, specificity and F1 score of all 0.86. All regression models performed well and the LightGBM model achieved the best results with r-square = 0.86, root mean squared error = 2.55 and mean absolute error = 1.86. Based on the interpretable SHAP analysis of the mentioned models, initial serum sodium, chloride, urine volume, blood urea nitrogen and glucose had essential effects on the patients’ following short-term serum sodium levels.

Conclusions：The proposed methods can accurately predict short-term serum sodium levels in the following 24-hour prediction window. And our methods can reasonably explain and visualization the prediction results utilizing clinical indicators.

models metrics

The 24-hour feature window contained serum sodium fluctuation, laboratory indicators, vital signs, drugs use, fluid intake/output. The upper part showed several situations of classification labels. The lower part showed the method of obtaining the label (Na2) of the regression window. The feature window of regression prediction was the same as the classification prediction.


models metrics

Flow chart of sample selection


models metrics

a SHAP values for the LightGBM model. This SHAP plot depicted the importance of each covariate in the development of the predictive model. b, c Scatter plots showed the relationship between feature values and SHAP values for Na1 (b) and chloride (c) of hyponatremia. d, e Scatter plots showed the relationship between feature values and SHAP values for Na1 (d) and chloride (e) of hypernatremia. The cut-off values were 137.5(b), 101(c),142.5(d) and 107(e).


models metrics

a Pearson correlations between LightGBM estimated values and true values (R2 = 0.8636) b Bland–Altman plots (mean = 0.0019, SD= 2.5535). The blue horizontal line near 0 represents the mean, the black dotted lines represent the 95% confidence interval.


models metrics

SHAP values for LightGBM regression model. Red indicated the feature was positive, blue indicated the feature was opposite. a Summary plot of all features SHAP values. b The average absolute values of the SHAP values of all the features corresponded to the subgraph a one-to-one. The larger the value, the greater the contribution of the feature to the model output. c The impact of each feature SHAP value on the model output for a random sample in the test set. For the convenience of observation, only the first ten features were drawn here. d The SHAP values of each feature of all samples on the test set. It was equivalent to the horizontal superposition of graph c of all the samples on the test set.